复平面计算本质和傅里叶变换
Author:张一极
date:2022年11月12日11:26:15
复平面
先验知识:
0.欧拉公式:
theta作为角度,可以换成跟时间有关的其他变量,比如,可以表示一个圆心角随时间变化情况。
1.复数乘法:
一般式:
2.根据欧拉公式复数乘法的极坐标系写法:
二者相乘得到:
即,复数极坐标中相乘可以表示为:幅角相加,模长相乘,所以这时候我们在推广到,单位复数的平方,即,其实就是因为,幅度相加,每一个i都在虚轴上一个单位长,一个i旋转90,两个i就旋转到180度,即-1。
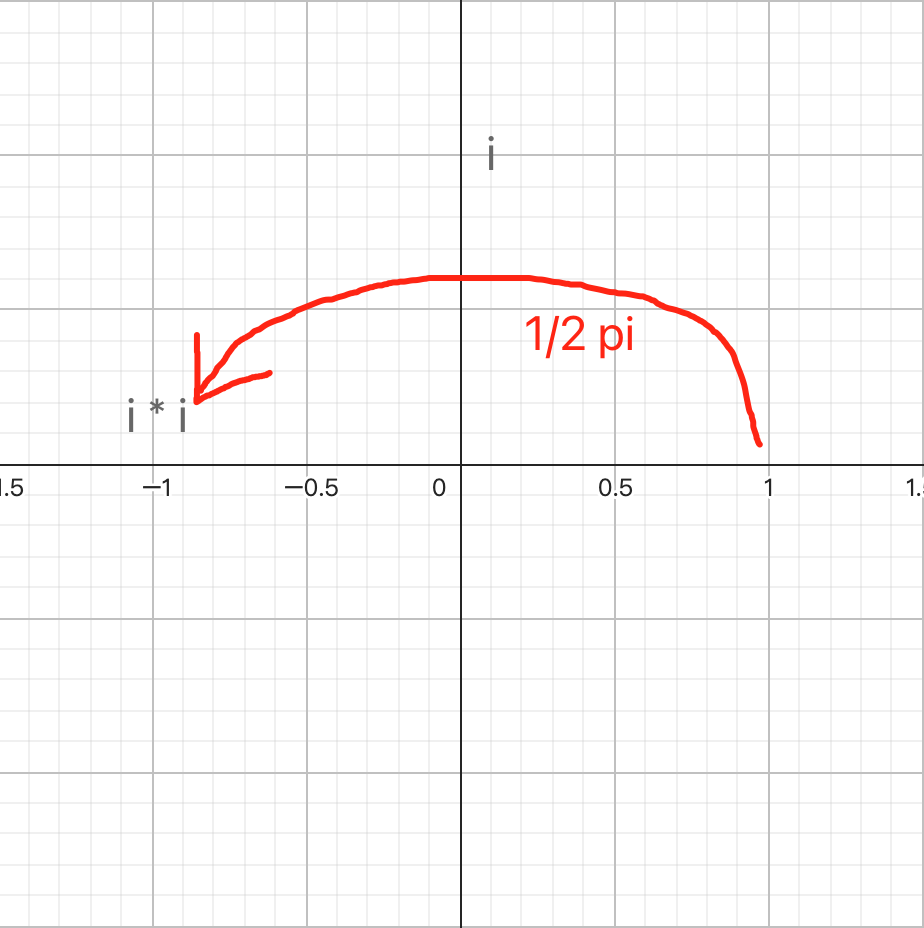
theta为幅角,i幅角为90:
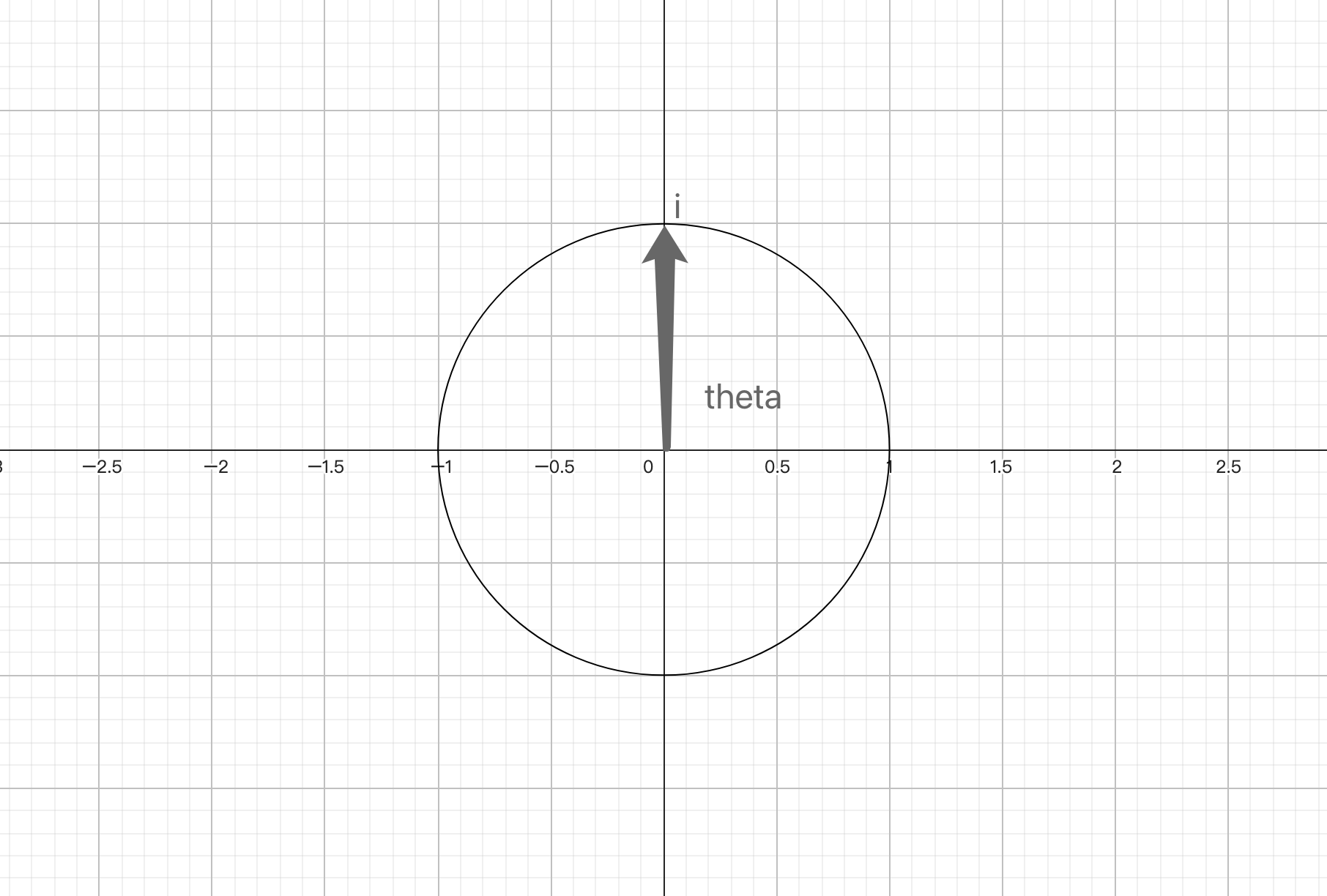
欧拉公式
以及:
用复数,表达旋转,或表达周期函数,可以表达任意频率,以及方向的周期函数。
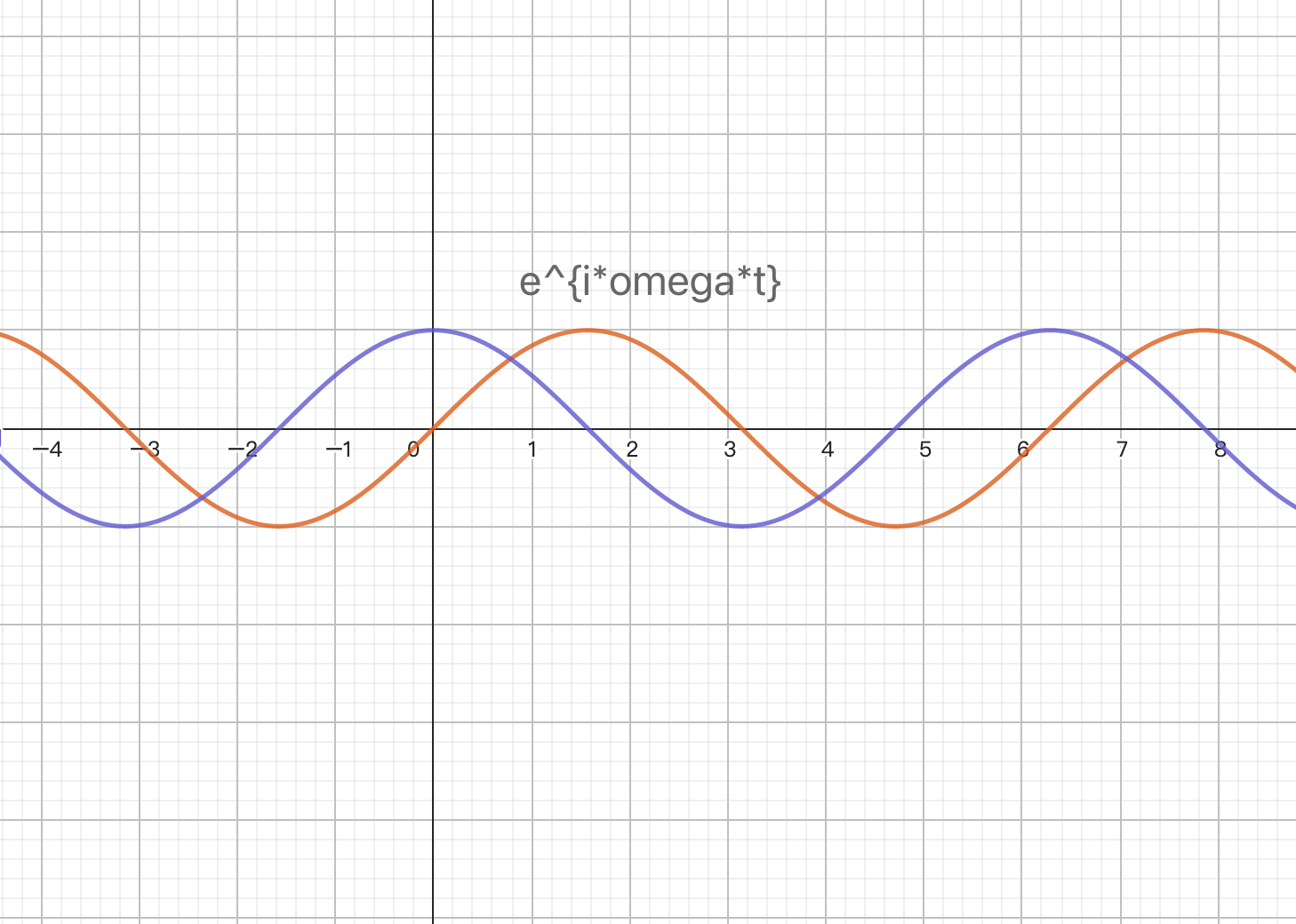
这时候的傅立叶变换
定义(来自维基百科):Fourier transform integral
其中,为模长, 表示了一个点,以每秒一圈的频率,即频率为1绕着圆心旋转,那么就代表了一个点,顺时针旋转,频率为ξ,可以认为是时间,或者任意其他的变换量,它影响着总体旋转的点位,则表示一个频率为ξ,逆时针旋转的点,结合欧拉公式中,可以认为,其中的。
傅里叶变换的本质是在说明,每一个复杂函数,都可以被n个组成,其表现形式即,把每一个分子做积分,从最小(负无穷)积到最大(正无穷)。


