欧拉公式的一般式推广:
Author:张一极
date:2022年11月13日08:41:53
本文目的:
证明上篇文章结论:
a.先验知识:定义
将极限带入:
把极限换到幂(常数为底):
洛必达法则(L'Hopital Rule),上下同时求导:
TO:↓
以上,可知:
推广到复数领域:
为求后项极限,将其中的阶乘部分,看做单个相乘,即n个
故
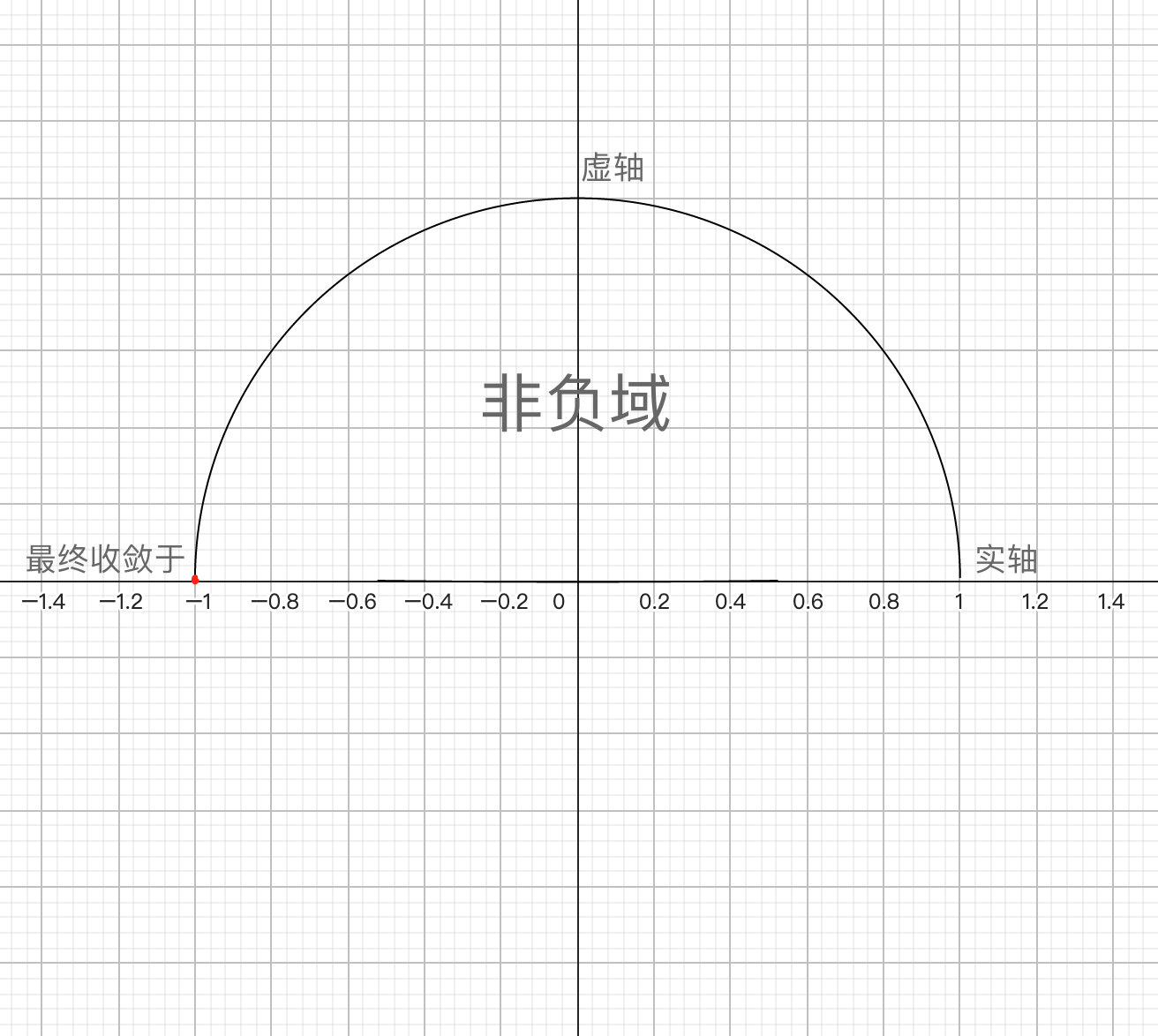
由此可知:
推广到一般形式,将
变化的部分为虚部,角度增量变成了
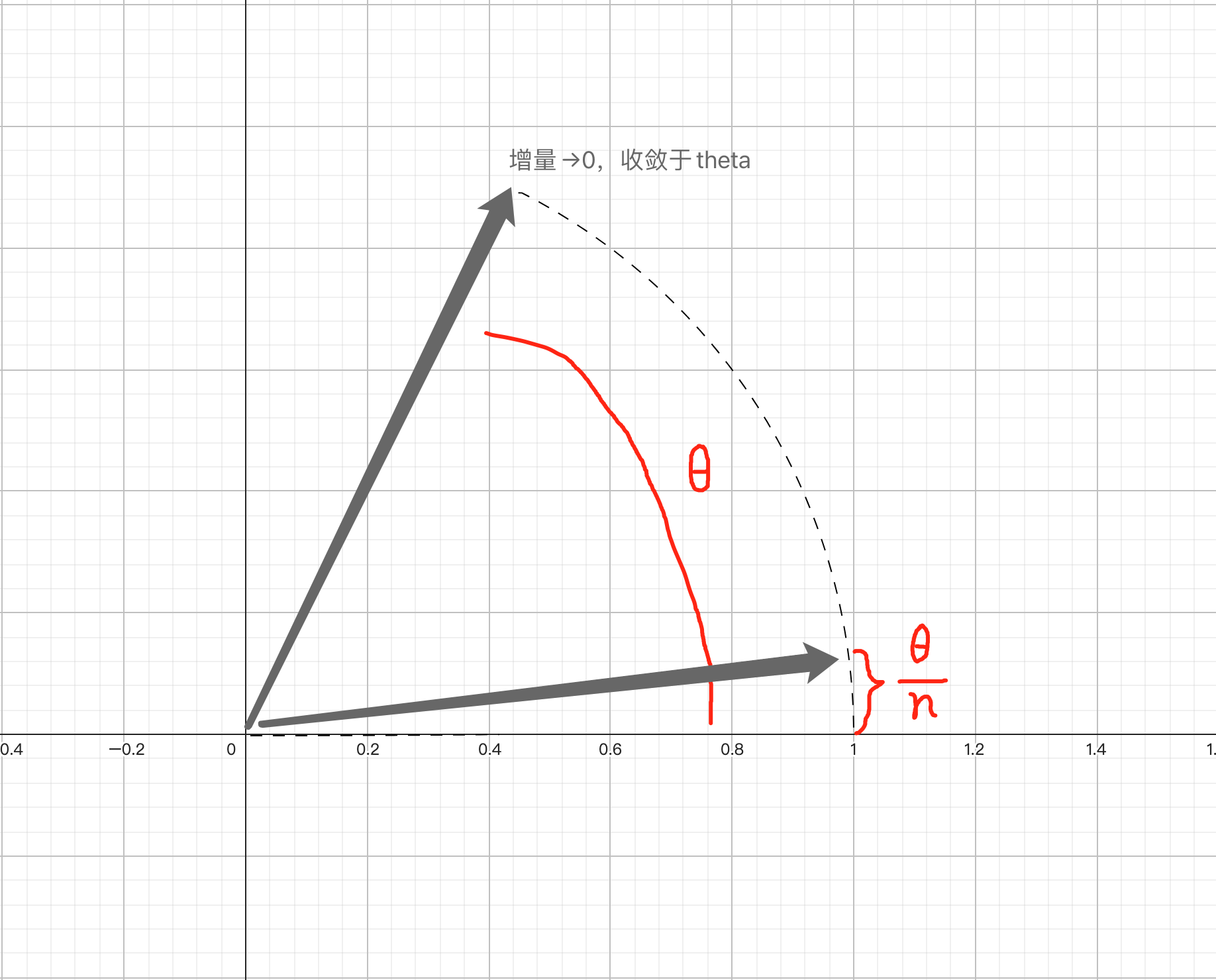
此时复平面上的点,即为
由此我们可以证明:
完成了实数平面到复平面的转换。
Author:张一极
date:2022年11月13日08:41:53
本文目的:
证明上篇文章结论:
a.先验知识:定义
将极限带入:
把极限换到幂(常数为底):
洛必达法则(L'Hopital Rule),上下同时求导:
TO:↓
以上,可知:
推广到复数领域:
为求后项极限,将其中的阶乘部分,看做单个相乘,即n个
故

由此可知:
推广到一般形式,将
变化的部分为虚部,角度增量变成了

此时复平面上的点,即为
由此我们可以证明:
完成了实数平面到复平面的转换。