Why prune or not to prune

Author：张一极

Email：[email protected]

引言

Deploying large, accurate deep learning models to resource-constrained computing environments such as mobile phones, smart cameras etc. for on-device inference poses a few key challenges

以上，便是模型剪枝领域重点关注的问题，即模型精度与模型开销的平衡问题。

Paper-1：

To prune, or not to prune: exploring the efficacy of pruning for model compression

——from Google

主要优化

模型压缩提出了两部分的优化，一个是内存密集部分的访问量，另外就是提高了获取模型参数的时间，即推理中的加载完毕时间。

主要实验

在模型压缩领域，我们通过清理不显著的连接参数，的确可以减少模型中非0参数的数量，并且不会对模型推理质量造成太大的影响，即使造成了影响，我们也能通过后续的微调调整回来。

文章首先测试了分类模型针对稀疏度的影响：利用tensorflow实现了对inceptionv3的模型剪枝，通过权重mask去遮盖剪枝完的权重，具体方法就是将得到权重在梯度下降的过程中，与mask点乘，屏蔽掉剪枝部分的梯度，不进行训练，同时这个mask会参与到模型的forward中，其中模型稀疏程度，通过下式定义：

其中for $t\in \{t_0,t_0+\mathrm{\Delta }t,\dots ,t_0+n\mathrm{\Delta }t\}$$t \in\left\{t_{0}, t_{0}+\Delta t, \ldots, t_{0}+n \Delta t\right\}$

其中 $s_i$$s_{i}$ 为初始稀疏率，通常为0，$s_f$$s_{f}$ 为最终稀疏率, $n$$n$ 为修剪总步数, $t$$t$ 为训练步数, $\mathrm{\Delta }t$$\Delta t$ 是修剪频率，一般为100到1000之间的数值。稀疏程度变化如图a，其训练过程，剪枝会在学习率还很高的时候开始，并且会在一开始很大幅度变化剪枝比例，越到后面，剪枝更倾向小修小改，而不是像刚开始一样大刀阔斧。

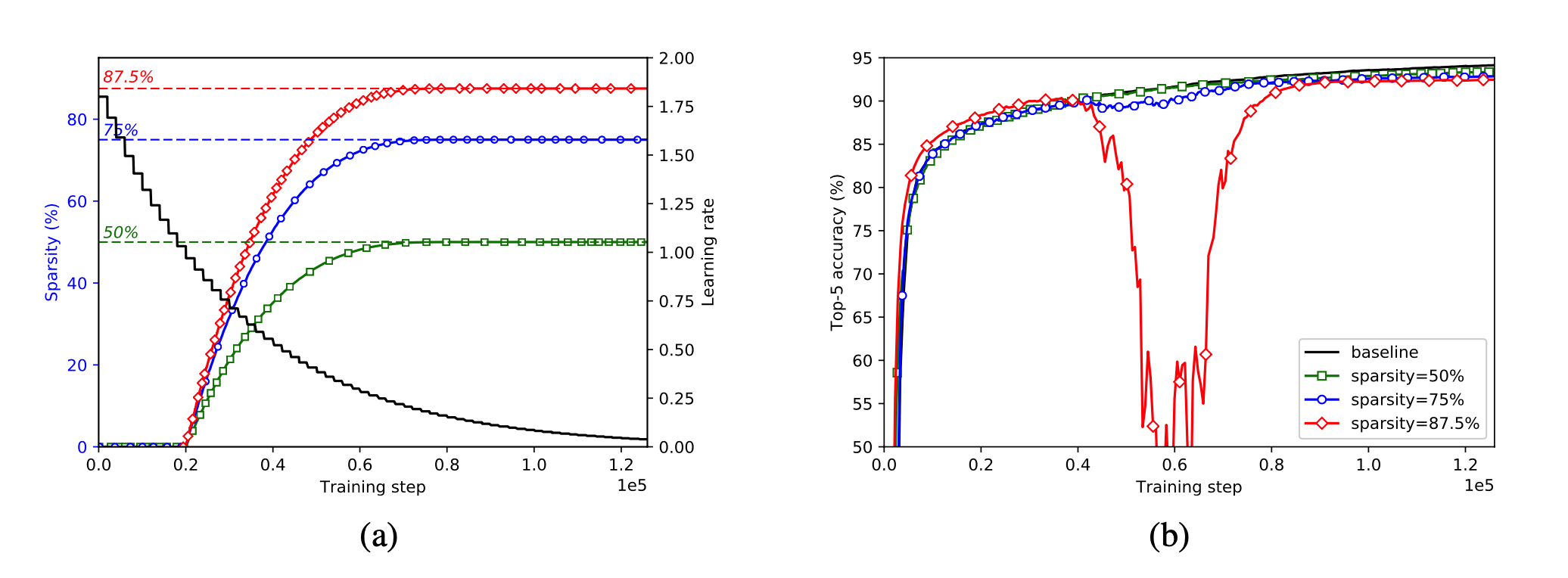
上图b中，分类网络inceptionv3的稀疏性不断提高，在稀疏程度达到87.5%的时候，训练过程中出现了一次准确率大幅下跌的情况，随后几乎以相同的速率，准确率回到了开始水平，此时我们可以推测稀疏掉的部分可能带有一部分核心权重，但是并不会影响到模型的拟合性能。通过微调几个epoch以后仍然能把模型恢复到较高水平，依然有着不低于baseline的拟合能力。

文章观察到修剪一个非常小的学习速率的存在使随后的训练步骤很难恢复精度损失，同时，学习率过高的剪枝可能意味着在权值尚未收敛的情况下将权值删除，所以才要一个与学习率相互影响的剪枝递进比例。

以下，是模型稀疏程度与acc的实验记录。

大而稀疏还是小而紧凑？

为了验证大而稀疏的模型与小而紧凑的模型优劣情况在分类任务下的分布。测试了mobilenet在不同稀疏程度和模型大小的情况下性能表现。

Mobilenet：

LSTM：

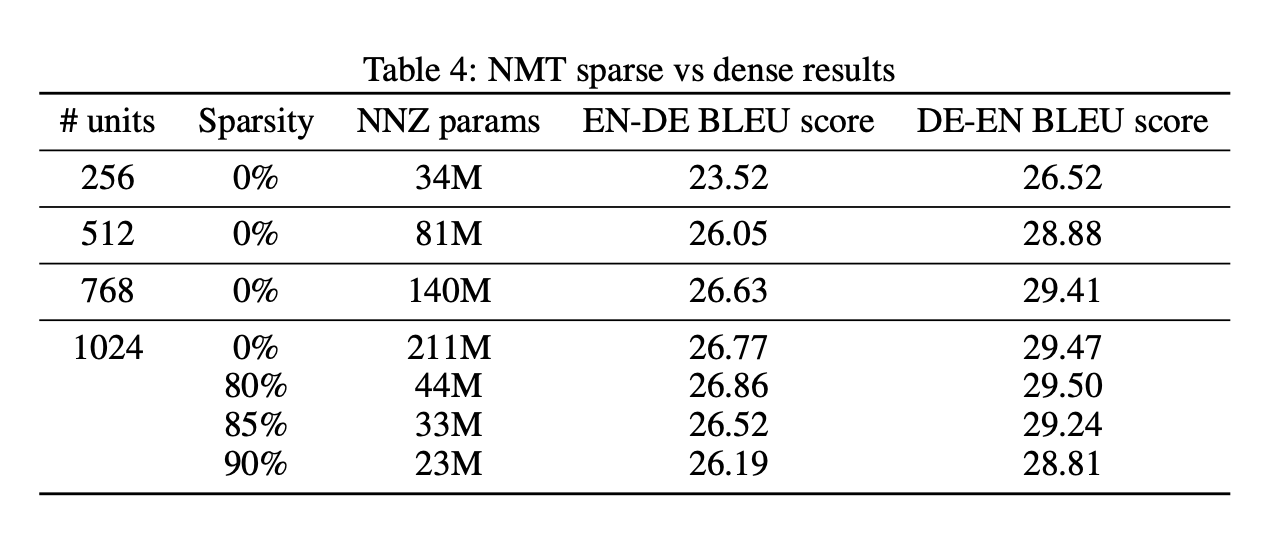
结论：

1.在内存占用相当的情况下，大稀疏模型比小密集模型实现了更高的精度，稀疏程度需要与学习率联动，保证整体流程不造成无法挽回的精度损失。

2.经过剪枝之后的稀疏大模型要优于同体积的非稀疏模型。

3.文中提出的递进剪枝策略可以广泛的应用于不同模型。

4.资源有限的情况下，剪枝是比较有效的模型压缩策略。

5.目前优化点还可以往硬件稀疏矩阵储存方向发展。

Paper-2：Lottery Ticket Hypothesis

The lottery ticket

文章提出了Lottery Ticket Hypothesis（以下简称LTH），验证了大部分密集，随机初始化的网络结构都有一个winnet ticket（以下简称wt），经过独立训练以后，在相同的迭代次数可以达到原有模型的精度水平，并且具有初始化的weight会使得训练收敛刚快。

文章提出了一种验证winner ticket的算法，讲述了验证实验过程。对于MNIST和CIFAR10这类小数据集来说，winner ticket得到的网络结构小于原有网络很多。且在这个大小的基础上，有winner ticket会让网络学习更快，达到更高的测试acc。

正式的假设：

More formally, consider a dense feed-forward neural network $f(x;\theta )$$f(x ; \theta)$ with initial parameters $\theta =$$\theta=$ ${\theta }_0\sim {\mathcal{D}}_{\theta }$$\theta_{0} \sim \mathcal{D}_{\theta}$. When optimizing with stochastic gradient descent (SGD) on a training set, $f$$f$ reaches minimum validation loss $l$$l$ at iteration $j$$j$ with test accuracy $a$$a$. In addition, consider training $f(x;m\odot \theta )$$f(x ; m \odot \theta)$ with a mask $m\in \{0,1{\}}^{|\theta |}$$m \in\{0,1\}^{|\theta|}$ on its parameters such that its initialization is $m\odot {\theta }_0$$m \odot \theta_{0}$. When optimizing with SGD on the same training set (with $m$$m$ fixed), $f$$f$ reaches minimum validation loss $l^{\prime }$$l^{\prime}$ at iteration $j^{\prime }$$j^{\prime}$ with test accuracy $a^{\prime }$$a^{\prime}$. The lottery ticket hypothesis predicts that $\mathrm{\exists }m$$\exists m$ for which $j^{\prime }\le j$$j^{\prime} \leq j$ (commensurate training time), $a^{\prime }\ge a$$a^{\prime} \geq a$ (commensurate accuracy), and $\parallel m{\parallel }_0\ll |\theta |$$\|m\|_{0} \ll|\theta|$ (fewer parameters).

主要步骤：

1.初始化一个随机的network

2.经过j次迭代

3.剪枝掉p%的权重参数，创建对应的掩码mask

4.重置参数到迭代后水平，清除剪枝参数，得到winner ticket

原文：

1. Randomly initialize a neural network $f(x;{\theta }_0)$$f\left(x ; \theta_{0}\right)$ (where ${\theta }_0\sim {\mathcal{D}}_{\theta }$$\theta_{0} \sim \mathcal{D}_{\theta}$ ).
2. Train the network for $j$$j$ iterations, arriving at parameters ${\theta }_j$$\theta_{j}$.
3. Prune $p\mathrm{\%}$$p \%$ of the parameters in ${\theta }_j$$\theta_{j}$, creating a mask $m$$m$.
4. Reset the remaining parameters to their values in ${\theta }_0$$\theta_{0}$, creating the winning ticket $f(x;m\odot {\theta }_0)$$f\left(x ; m \odot \theta_{0}\right)$.

通过迭代剪枝的方法，比一次性剪枝掉p%，更容易得到优秀的结构。

最终，文章测试了wt在不同数据集和初始化方式的表现，通过几种优化策略(SGD、momentum和Adam)，包含dropout、权值衰减等方法，在MNIST的fullconnect和CIFAR10的conv architectures中确定了wt。

接下来，文章进行了测试和总结，主要目的是，将假说拓展到任意表现优异的网络中，可以当成一个简易版的网络搜索过程，只不过没有进行网络结构的变化，只针对网络的超参数进行变化。

Fullconnect

将LTH假说应用在mnist的全连接网络上测试：

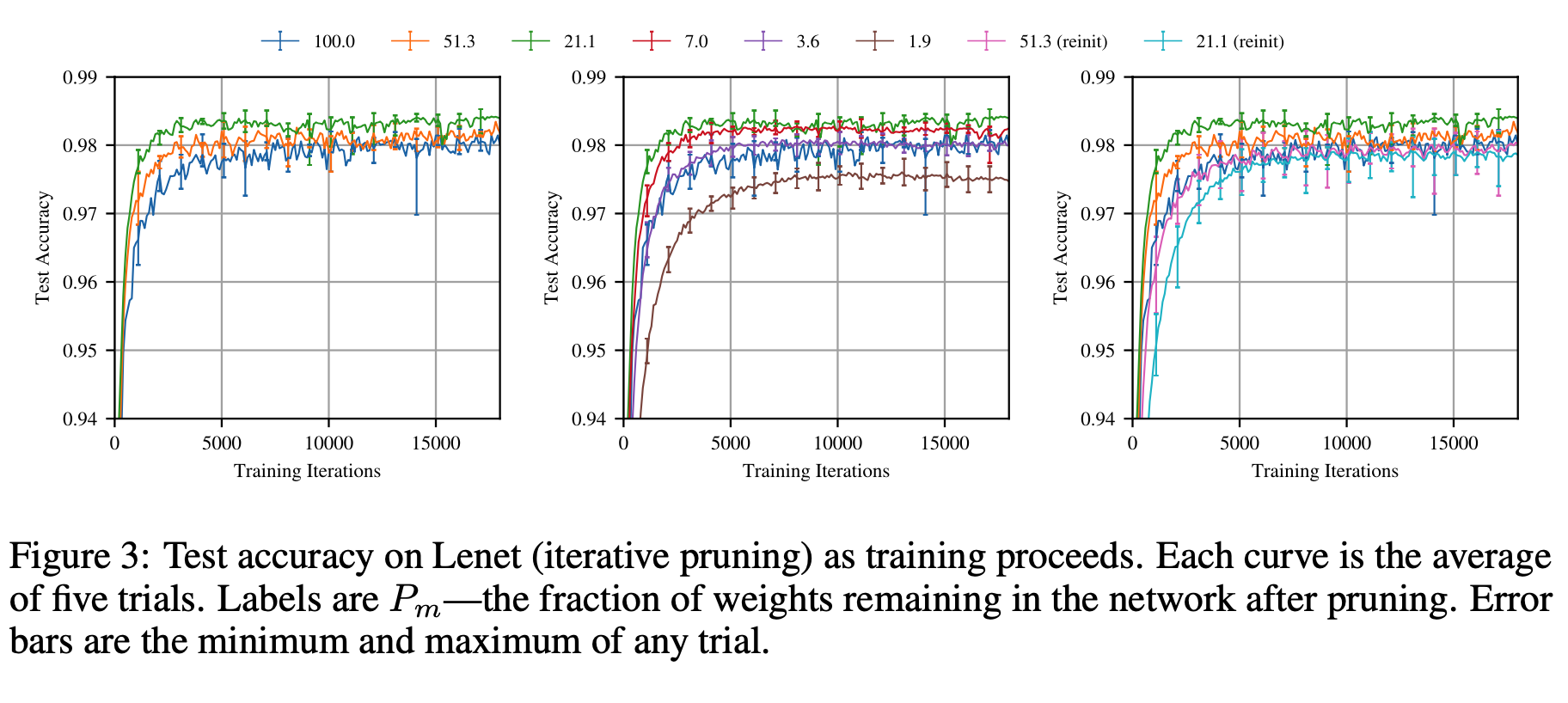
假如把原网络当作baseline可以看出，剪枝后的网络，收敛速度明显比baseline要快，除非是剪枝数量过大的棕色曲线（Figure3 b）随即初始化也是模型收敛比较慢的一个原因，对比试验可以看出，第三张图中蓝色21.1的曲线比初始化权重的21.1速度精度要低，且收敛速度更慢。

下图展示了wt（剪枝比例21.1%的子网络）的早停情况：

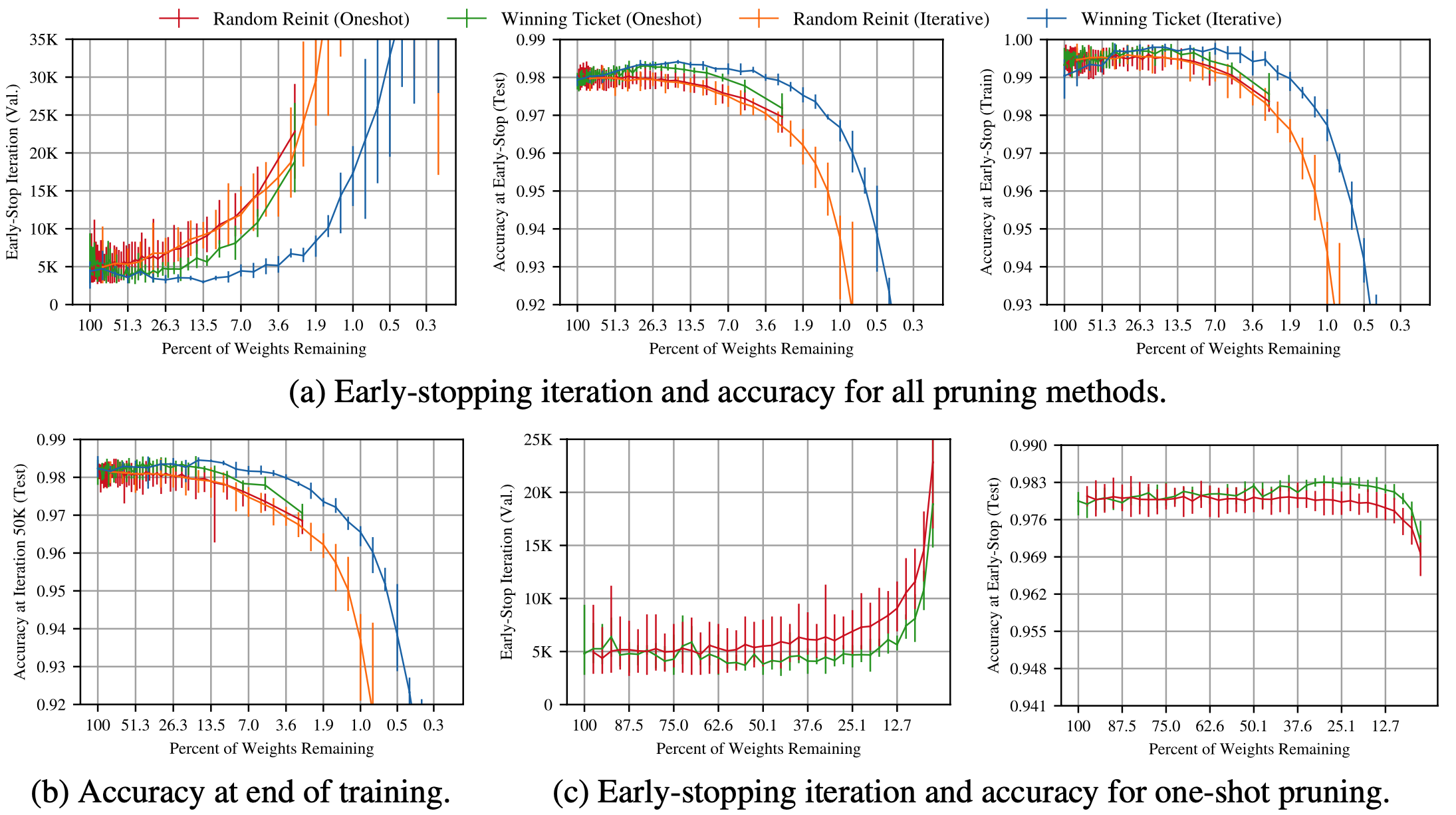
oneshot的剪枝策略，一次性剪枝到目标比例，比起渐进式的剪枝策略，收敛速度和acc都比较差，由此可以得出，多次反复剪枝，测试，会得到更精准优化的网络结构。

同时，在迭代修剪中，wt比原始网络收敛更快，作者还做了一个实验，把几个模型一起训练到收敛，training精度100%，此时prune掉2%以上的网络结构，发现对wt的精度影响最小：

本次实验说明了wt在拟合训练集于测试集上，有着更好的泛化性能。

作者还测试添加了dropout的效果：

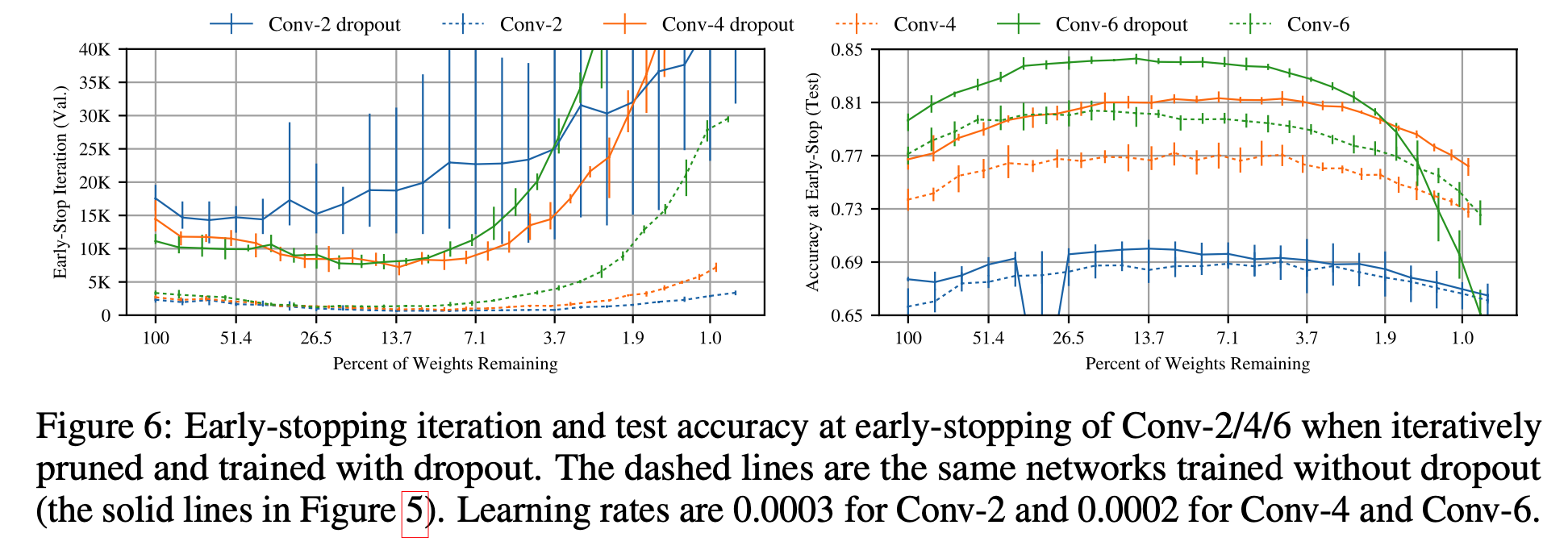
作者认为自己的迭代剪枝方法与dropout有着相互补充的作用，某些不必要得权重留下来以后，很容易被dropout清理掉，另一方面，有些dropout漏掉的低贡献权重，会被prune清理掉。

大概总结一下文章表达的看法：

1.The importance of winning ticket initialization.wt的初始化如果是随机的话，会导致学习效率降低且表现损失。

2.The importance of winning ticket structure.

3.The improved generalization of winning tickets

4.Implications for neural network optimization.

每个网络结构都有其修建完成以后最优的子网，不断迭代剪枝。

Paper-3 L1范数剪枝

针对每一个conv卷积核计算一个L1范数

按照sj的排序，删除最小的几个卷积核，删除卷积核的输出feature map，以及下一层对应上层被删除featuremap的卷积核。

x
1
def channels_index(weight_matrix, prune_num, residue, independentflag):
2
    abs_sum = torch.sum(torch.abs(weight_matrix.view(weight_matrix.size(0), -1)), dim=1)
3
    _, indices = torch.sort(abs_sum)
4
    return indices[:prune_num].tolist()

17
1
def prune_vgg(net, independentflag, prune_layers, prune_channels):
2
...
3
    for i in range(len(net.module.features)):
4
        if isinstance(net.module.features[i], nn.Conv2d):
5
            if last_prune_flag:
6
                net.module.features[i], residue = get_new_conv(net.module.features[i], remove_channels, 1)
7
                last_prune_flag = 0
8
            if "conv_%d" % conv_index in prune_layers:
9
                remove_channels = channels_index(net.module.features[i].weight.data, prune_channels[arg_index], residue,independentflag)
10
                net.module.features[i] = get_new_conv(net.module.features[i], remove_channels, 0)
11
...
12
            conv_index += 1
13
        elif isinstance(net.module.features[i], nn.BatchNorm2d) and last_prune_flag:
14
            net.module.features[i] = get_new_norm(net.module.features[i], remove_channels)
15
    if "conv_13" in prune_layers:
16
        net.module.classifier[0] = get_new_linear(net.module.classifier[0], remove_channels)
17
    return net

4
1
from nni.algorithms.compression.pytorch.pruning import L1FilterPruner
2
config_list = [{ 'sparsity': 0.8, 'op_types': ['Conv2d'] }]
3
pruner = L1FilterPruner(model, config_list)
4
pruner.compress()